Least Significant Bit, 模数转换, 主要参考以下内容
What is an LSB? The LSB is the smallest level that an ADC can convert, or is the smallest increment a DAC outputs.
The ADC needs a voltage reference to convert an analog signal into a digital word. Depending on the number of bits it has, the ADC divides the voltage reference in small levels called counts. For example, if this is an 8-bit ADC, the counts will look like those in Figure 1. In an 8-bit ADC there are 28 = 256 counts.

One count is 1 LSB, and is defined as follows:
$$ \mathrm{LSB}=\frac{\mathrm{Vref}}{2^{\mathrm{N}}} $$ where N is the ADC’s or DAC’s number of bits. For ADCs that have a differential voltage reference, the LSB is
$$ \mathrm{LSB}=\frac{\mathrm{Vref}(+)-\mathrm{Vref}(-)}{2^{\mathrm{N}}} $$
where Vref(+) and Vref(-) are the non-inverting and the inverting inputs of the differential voltage reference respectively.
The ADC outputs a digital word that shows how many counts are in its input voltage level. As the ADC counts the input level, it never reaches the voltage reference. Its full scale (FS) is calculated with the following formula:
$$ \mathrm{FS}=\mathrm{Vref}-1\cdot\mathrm{LSB} $$
After replacing the LSB in equation, the ADC full-scale results as in following equation.
$$ \mathrm{FS}=\mathrm{Vref}\cdot\frac{2^{N}:-1}{2^{N}} $$
Figure 2 shows the ADC counts and the corresponding hex code.
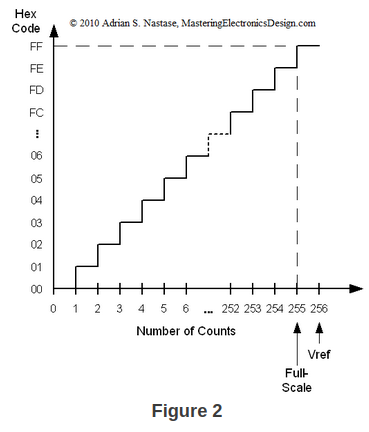
As you can see, and ADC can never reach its Vref but, as the number of bits is higher, it gets very close to its referencc voltage. The same can be said about a DAC. Moreover, from equation (1), we can write the mathematical relation between Vref and LSB as follows:
$$\mathrm{Vref}= 2^{\mathrm{N} }\cdot \mathrm {LSB} $$ if we replace Vref in equation, and after calculations, we can write the definition of the LSB as a function of the ADC’s full-scale, as in equalion (7).
$$ \mathrm{LSB}=\frac{\mathrm{FS}}{2^{\mathrm{N}}-1} $$
This is the trouble, as the LSB has two definitions. Both of them are valid, and some authors are ambiquous or confused about them. I have seen articles in which Vref is considered the component full-scale, which is the premise that qenerates subsequent wrong definitions.



